INTRODUCCIÓN
Al inicio del segundo periodo del 2011, exactamente el día martes 16 de agosto comenzamos a estudiar la asignatura de investigación de operaciones II. Ésta materia es dictada por el profesor Jairo R. Coronado Hernández, Ingeniero Industrial de la Universidad Tecnológica de Bolívar.
En ésta clase, el profesor procedió a hacer su presentación personal y luego nos hizo presentarnos a todos. Posteriormente, comenzó a explicar la relación que tiene la investigación de operaciones II con la Ingeniería Industrial.
Para comenzar con las enseñanzas respectivas, vimos temas como: la teoría de decisiones, el árbol de decisión y las funciones de utilidad. Los cuales están muy relacionados con las alternativas de decisión y la incertidumbre que puede generar dicha decisión.
A continuación, veremos una breve explicación de los temas expuestos en todas las clases vistas hasta el día 20 de septiembre.
CLASE # 1
CLASE # 1
TEORÍA DE DECISIONES
La teoría de decisiones consiste en la toma de la mejor decisión para nuestro mayor beneficio. Existen tres tipos de toma de decisiones, los cuales son:
Bajo certidumbre
Es un tipo de decisión en la cual, se conocen todos los datos del problema propuesto.
Bajo riesgo
Tipo de decisión en la cual se conocen los datos del problema propuesto, pero con una distribución de probabilidad, ya sea positiva o negativa.
Bajo incertidumbre
En esta, no se conocen los datos del problema propuesto.
Problemas relacionados
· Dieta
· Transporte
Existen diferentes criterios de análisis en la toma de decisiones bajo certidumbre, los cuales son:
LAPLACE
Consiste en una hipótesis optimista.
MINIMAX(MAXIMIN)
Consiste en una hipótesis pesimista, es decir, minimizar la máxima pérdida o maximizar la mínima ganancia.
SAVAGE
Criterio de pesadumbre o de arrepentimiento. En éste, se utiliza el criterio Minimax (Maximin).
HURWICZ
Consiste en la toma de decisiones, de la más optimista a la más pesimista.
En la toma de decisiones bajo riego, no hay criterios de análisis todo se hace con distribución de probabilidad (árbol de decisión). Ahora, veamos un ejemplo de un problema y la resolución de éste con su respectivo grafico, para un mejor entendimiento sobre el concepto de árbol de decisión:
Suponga que se desea invertir $10000 en el mercado de valores, comprando acciones de una de dos compañías: A y B. Las acciones de la compañía A son arriesgadas, pero podrían producir un rendimiento de
50% sobre la inversión en el próximo año. Si las condiciones del mercad de valores no son favorables (Mercado a la baja), las acciones pueden perder el 20% de su valor. La empresa B proporciona utilidades seguras, de 15% en un mercado a la alza y solo un 5% en un mercado a la baja. Según las publicaciones consultadas se predicen que hay un 60% de probabilidades que el mercado este en alza y el 40% de que este a la baja. ¿Dónde debería invertirse el dinero?
La mejor decisión que se debe tomar, es invertir el dinero en A, ya que la probabilidad es mayor que la de B.
Este ejemplo fue tomado de http://aulas.utbvirtual.edu.co/file.php/9777/Clase_1_-_Teoria_de_decisiones.pdf
Para finalizar con esta clase, el profesor nos dejo un trabajo por realizar, que consistía en cómo utilizar las funciones de utilidad bajo árbol de decisión, y nos recomendó utilizar el programa “TREEAGE” para la realización de éste.
 Modelos clásicos
Modelos clásicos
CLASE # 2
PROGRAMACION MATEMATICA EN MODELOS ENTEROS MIXTOS
El día martes 23 de agosto estuvimos aprendiendo sobre la Programación Entera, que es un término general para los modelos de programación matemática que presentan condiciones de integridad (condiciones que estipulan que algunas o todas las variables de decisión deben tener valores enteros). Ya hemos apuntado que los modelos de programación lineal entera son modelos de programación lineal que tienen la característica adicional de que algunas de las variables de decisión deben tener valores enteros.
Programación entera es programación lineal con la restricción adicional de que los valores de las variables de decisión sean enteros.
P.E. Binaria (PEB): Utiliza variables binarias
Sólo tiene 2 alternativas posibles
Xj= 1 si la decisión j es sí.
0 si la decisión j es no.
Las Xj son variables de decisión restringidas a tomar valores 0,1.
En ocasiones es necesario utilizar variables para expresar relaciones combinatorias dentro de la formulación de los problemas. Para esto, además de las variables originales Xj, se hace necesario el uso de variables auxiliares yidel tipo binario, introducidas en la reformulación.
· Modelando múltiples periodos
Muchas veces se requiere modelar el proceso de planificación teniendo en cuenta un número de periodos a futuro
· Restricciones de precedencia
Una tarea no puede comenzar hasta que finalice la anterior tarea.
· Una u otra restricción
Sólo una (cualquiera de las 2) debe cumplirse, mientras que la otra puede cumplirse, pero no se requiere que lo haga. Esto tiene una aplicación práctica en los casos en que se tienen 2 tipos de recursos para un cierto propósito.
· K de N restricciones
Considere la situación en la que el modelo completo incluye un conjunto de N restricciones posibles entre las que sólo K de ellas se deben cumplir. (Supongaque K < N). Las N-K restricciones que no se eligen quedan eliminadas del problema, aun cuando por coincidencia las soluciones factibles puedan satisfacer algunas de ellas.
· Funciones con n-valores positivos
Considere la situación en la que una función dada tome cualquiera de N valores dados. El lado derecho puede tomar diferentes valores dependiendo del uso de los recursos.
· Decisiones sí o no
Existen problemas de programación lineal en donde las variables están seguidas de una decisión. Las restricciones nos dicen que si escogemos una variable entonces la otra estará relacionada con esa decisión.
· Modelos de distribución con costos de apertura
Este modelo tiene los siguientes índices y conjuntos
i€I plantas productivas
j€J clientes
Contiene los siguientes parámetros
Las variables de este modelo se plantean asi:
0 no se abre
· Modelo de la planificación de la producción
Una unidad global lógica para medir las ventas y la producción.
Pronosticar la demanda para el periodo de planificación intermedio es estas unidades agregadas.
Un método para calcular los costes.
Un modelo que combine los pronósticos y los costes para que puedan tomarse buenas decisiones de programación para el periodo de planificación.
· Modelo de programación de la producción
Modelo en donde se toman como restricciones el tiempo de proceso del trabajo, tiempo de entrega del trabajo, tiempo de alistamiento de pasar de un trabajo a otro. Contiene unas variables las cuales incluye tiempo de determinación del trabajo, tardanza del trabajo, tiempo de inicio del trabajo.
CLASE # 3
Día 30 del mes de agosto de año 2011 a la hora 1:15pm, se realizo la clase de investigación de operaciones 2 en el salón 503, del bloque A2, de la Universidad Tecnológica de Bolívar campus de ternera, el ingeniero Jairo Coronado inició la clase hablando sobre la continuación del tema que habíamos dejado en la clase anterior de programación matemática de modelos enteros mixtos, principalmente sobre los modelos básicos.
Nuestro tercer ejemplo fue el Modelo de programación de la producción, el cual tiene como índices: conjunto de trabajo (i) y (j=i), también consta de parámetros y variables, y a partir de éste se obtienen la función objetivo y las variables.
Estos ejemplos están resueltos en: http://aulas.utbvirtual.edu.co/file.php/9777/Clase_2_-_Programacion_matematica_en_modelos_enteros_mixtos.pdf
Un problema de programación lineal consiste en hallar el valor óptimo de una función objetivo lineal cuyas variables están sujetas a restricciones lineales. Para nosotros dar solución a los modelos que se iban a mostrar más adelante no solamente debían ser lineales, además se exigía que las variables tomaran valores enteros, entonces si teníamos un problema de programación lineal-entera.
Comenzamos a observar los ejemplos de modelos. El primero fue Modelo de distribución con costos de apertura, donde los índices de éste son los clientes (j) y las plantas de producción (i), se tenían unos parámetros y unas variables, y a partir de estos datos se obtenía una función objetivo y una serie de restricciones para que se cumpliera dicho modelo.
Más adelante observamos otro ejemplo que era el Modelo de planificación de la producción, donde sus índices eran periodos (t), productos (i) y maquinas (r), cuyo objetivo es determinar el número del producto (i) a fabricar en la maquina (r) en el periodo (t). Éste como el anterior, también tiene parámetros y variables, y a partir de estos se obtenía la función objetivo y las restricciones. En éste se presentaron otros tipos de restricciones que se debían cumplir y pasaron varios compañeros a resolverlas, tal como: un solo producto se debía hacer en una sola maquina.
Después de explicar éstos ejemplos, el profesor colocó un modelo para que lo resolviéramos en clase con la ayuda de nuestros compañeros, el cual era de transbordo de i plantas, j bodegas y k clientes, como se muestra en la siguiente imagen:
Donde los productos de las plantas solo podían ir a solo una de las bodegas para que fuese repartido a los clientes.
Donde parte de la solución fue la siguiente:
· Conjunto:
i = producto.
J = bodega
T = periodo
· Parámetros:
Capi = capacidad de producción del producto i
Cij = costo de trasporte de i a j
C2jk = costo de trasporte de i a k
Dk = demanda del cliente
Cfj = costos fijos
· Variables:
Xij = numero de productos i llevados a j
Yik = numero de productos i entregados al cliente k
Nos pudimos dar cuenta que estos modelos tienen numerosas aplicaciones a problemas que se presentan en la industria, logística, ciencias, ingenierías y en la administración de organizaciones. Como ejemplos podemos mencionar, entre otros, el ruteo y carga de vehículos en redes de distribución, el diseño de redes de telecomunicación, la planificación de la producción entre otros.
CLASE # 4
El día martes 6 de septiembre de 2011 el profesor no pudo asistir a clases, ya que tuvo que ir a un evento en el centro de convenciones y nos dijo a las 12:30 pm en SAVIO lo siguiente:
“Queridos Alumnos.
Espero se encuentren bien. Lamentablemente no voy a poder acompañarlos en la clase de hoy, porque me encuentro en un evento en el Centro de Convenciones.
Dejen sus ensayos con la secretaria de ingeniería industrial, lo pueden dejar mañana por si no vieron el mensaje a tiempo. El parcial lo haremos el día 20 de septiembre.
Después recuperaremos la clase. Disculpen mi inasistencia y el no informarles a tiempo.
Un saludo,
Jairo R. Coronado-Hernández.”
Los ensayos que teníamos que entregar tenían que ver con el tema del problema del agente viajero, descripción del modelo, solución, etc.
CLASE # 5
El día martes 13 de septiembre de 2011 todos los estudiantes nos dirigimos al salón A2 503 como de costumbre, esperamos al profesor, pero cuando este llegó nos dijo que nos trasladáramos hacia el edificio A1 en el cuarto piso, a un salón que tiene computadores, debido que los necesitábamos para poder aprender la forma en la cual se debe utilizar el programa AIMMS.
Al llegar a nuestro destino nos dijo el encargado de los salones que todos estaban ocupados, así que nos tocó irnos para los laboratorios de ingeniería industrial.
En el laboratorio, ya todos ubicados comenzamos a instalar el programa en cada computador y luego vino la explicación, a cargo del estudiante Joned Chica.
Primero que todo, escribió el modelo de transporte en el tablero:
Modelo de transporte:
Luego de esto, inició la explicación de códigos y métodos de pasar el ejercicio del papel al computador, es decir, explicó la forma de utilizar el programa AIMMS. Aquí veremos unos cuantos códigos de tantos que hay en el programa, por ejemplo:
Conjunto - Set
Parámetro – Param
Variable – Var
∑ - sum[(ij)]
≥ - >=
≤ - <=
Con este ejercicio terminamos de utilizar AIMMS y el profesor continuó el resto de la clase con la explicación del tema Branch and Bound.
Branch and bound se caracteriza por solucionar un problema pero con un alto costo computacional, genera un árbol de expansión binaria y es utilizado para dividir y conquistar.
Este método consiste en ramificar y podar, cuando la solución al problema es factible pero no es entera, entonces se ramifica para llegar a una solución entera; y cuando no es factible se poda. Existen tres formas de podar:
a) Por infactibilidad.
b) Al comparar las cotas y la anterior tiene un mejor resultado en la función objetivo, se corta la rama.
c) Cuando la solución es entera (integrabilidad)
Los ejercicios de dicho tema fueron realizados en la siguiente clase.
CLASE N° 6
CLASE N° 6
El día 20 de septiembre de 2011 fue nuestra clase N° 6, dicha clase se dio 2 días antes del primer parcial de investigación de operaciones II.
En esta clase estuvimos realizando un ejercicio del libro TAHA 7ª. Edición que se encuentra en la sección de problemas 9.2B – ejercicio N° 6 – pagina 383. Para practicar el método de branch & bound.
El ejercicio es el siguiente:
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
Como el ejercicio es de 3 variables X1, X2, X3 entonces procedemos a realzarlo por el algoritmo simplex.
Convertimos las desigualdades en igualdad mediante la introducción de variables de holgura o variables de exceso.
Si existen restricciones de la forma (=) y/o (≥) utilizar variables artificiales T (i)
Presentamos la solución del problema mediante las tablas del software WinQSB
Solución
Nos damos cuenta que la solución es X1 = 0, X2 = 2,5 Y X3 = 0 con Z = 5
Como X2 no cumple con la condición de enteros entonces ramificamos.
Ahora nos tenemos dos nuevos problemas con una restricción nueva cada uno, X2 ≤2 y X2 ≥ 3 respectivamente.
Resolvemos el problema con la ramificación que es X2 ≥ 3
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≥ 3
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
Ahora solucionemos el nuevo problema
Nueva Solución
Esta solución es: X1 = 0, X2 = 3, X3 = 0,6 con Z = 4
Entonces podamos esta rama ya que X1, X2 son enteros y procedemos a solucionar la ramificación de
X2 ≤2
Ahora para resolver la otra rama tenemos que incluir la restricción X2 ≤2, entonces el problema nos queda de la siguiente manera:
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≤2
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
La solución de este problema es:
Podemos ver que la solución es: X1 = 0,6 X2 = 2, X3 = 0 con Z = 4,6. Ahora nos tocaría ramificar X1= 0,6 ya que no es entero, entonces el árbol de ramificación quedaría así:
Ahora tenemos dos restricciones nuevas que serian X1≤0 y X1≥1. Procedemos a resolver el problema con cada restricción
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≤2
X1≤0
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
La solución de este seria:
La cual nos indica que X1 = 0, X2 = 2, X3 = 0 con Z = 4.
Aquí encontramos una solución entera pero no es la solución final, ya que nos falta una rama que es X1≥1 y además no hay cotas superiores ya que en las 2 soluciones enteras que se han encontrado Z = 4 por lo tanto procedemos a resolver el otro nodo de X1≥1 y nuestro árbol estaría de la siguiente forma:
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≤2
X1≥1
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
La solución del problema con esta nueva restricción seria:
La solución es: X1=1, X2=1,7 X3= 0 con Z= 4,5.
Tenemos que ramificar a X2= 1,7 en X2≤1 y X2≥2, entonces nuestro árbol quedaría de la siguiente forma:
Ahora resolvamos el problema incluyendo la restricción X2≤1
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≤2
X1≥1
X2≤1
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
La solución de este es:
Entonces vemos que la solución es entera porque X1=2, X2=1, X3=0 con Z=4 y seguimos teniendo el mismo resultado de Z=4 lo cual quiere decir que no tenemos ninguna cota superior a esta. Podamos esta rama y solucionamos el siguiente nodo de tal manera que nuestro árbol esta de la siguiente manera:
MAXIMIZAR Z = X1 + 2 X2 - 3 X3
Sujeto a:
3 X1 + 4 X2 - 3 X3 ≤ 10
2 X1 - 3 X2 + 4 X3 ≤ 20
X2 ≤2
X1≥1
X2≥2
X1, X2 ϵ enteros
X1, X2, X3 ≥ 0
La solución de este problema es:
Vemos que la solución es X1=1, X2=2, X3= 0,33 con Z=4, lo cual quiere decir que la solución es entera y por lo tanto podamos la rama, pero vemos que todas las 4 soluciones enteras que encontramos tienen Z=4 entonces podríamos decir que el problema tiene soluciones infinitas.
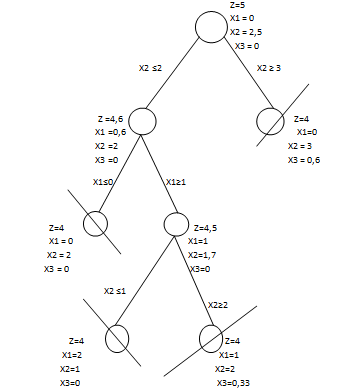
Ahora nuestro árbol finaliza de la siguiente manera:
El problema tiene múltiples soluciones